こんにちは、ゆうじ(@yuji_sgs_prog)です。
機械学習のアウトプットでまとめた内容についての解説記事です。
上記の記事で全てをまとめると大変なので、今回個別の記事でまとめていきます。
Kerasを活用して、ニューラルネットワークによる回帰分析を行いたい方は参考になると思うので、ぜひご覧ください。
理系の大学・大学院生は「TECH-BASE」による機械学習スキルの習得がおすすめです。カリキュラムから学習支援、就活のサポートまで全て無料で受講できるため、お得に市場価値の高いスキルを身につけてキャリア形成に役立てていきましょう。
Kerasで回帰ニューラルネットワークを実装する前に
まずは、いきなりモデルの解説に入るのではなく、事前準備や環境について紹介していきます。
- Google Colaboratoryにて実行
- データセットは3列×10,000行のcsvデータ(自前csvファイルはこちら。※クリックするとダウンロードします)
- 一番単純かつシンプルなSequentialモデルを構築
実行環境についてはJupyter Notebookなどでも良いですが、Google Colabratoryなら無料でGPUが使えるので、適当に使ってます。
また、データセットについて1, 2列目をインプットに、3列目をアウトプットとしてニューラルネットワークを構築していきます。
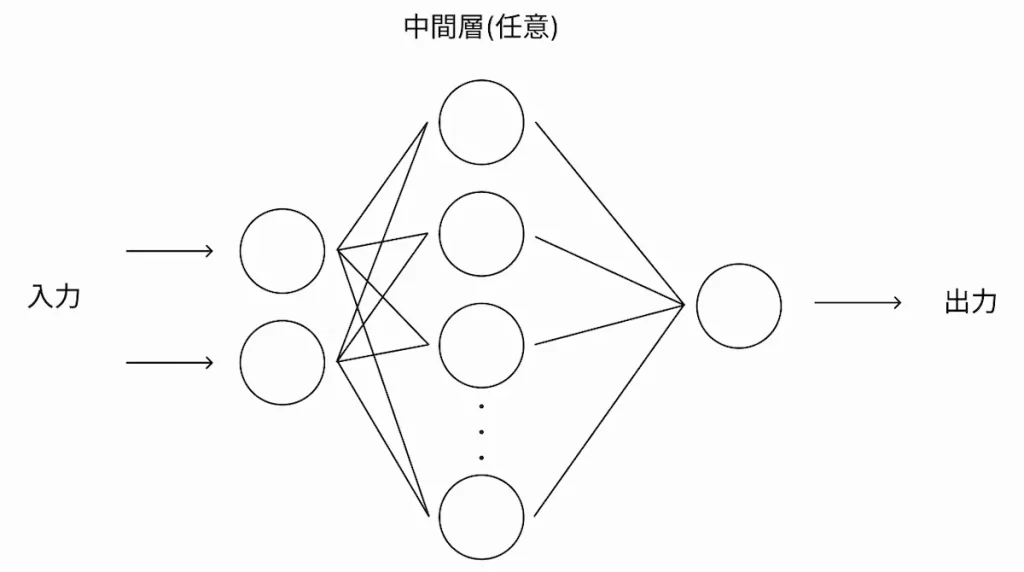
Kerasで回帰ニューラルネットワークを実装したコードを解説

実装したコードの全体像をまず紹介していきます。
なお、実装したコードはipynb形式でGitHubに上げているので、そちらも参考にしていただければと思います。
# 使用するライブラリをインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import io
from google.colab import files
from sklearn.model_selection import train_test_split
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import Adam
from keras.callbacks import EarlyStopping, LearningRateScheduler
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from math import sqrt
from sklearn.metrics import r2_score
# Google Colaboratoryでファイルをアップロード
uploaded = files.upload()
# データフレームとして、変数dfに3列×10000行のデータを格納・確認
df = pd.read_csv(io.BytesIO(uploaded['data.csv']))
df
# データの分割
(train, test) = train_test_split(df, test_size=0.2, shuffle=True)
# x_train, x_testではcsvファイルの1列目から2列目を,y_train, y_testでは3列目のデータを活用
x_train = train.iloc[:, [0, 1]]
y_train = train.iloc[:, [2]]
x_test = test.iloc[:, [0, 1]]
y_test = test.iloc[:, [2]]
# データの正規化
x_train = (x_train - x_train.min()) / (x_train.max() - x_train.min())
x_test = (x_test - x_test.min()) / (x_test.max() - x_test.min())
# モデルの構築
# inputの数
n_in = 2
# ノードの数
n_hidden = 16
# outputの数
n_out = 1
# 学習回数
epochs = 50
batch_size = 64
model = Sequential()
model.add(Dense(n_hidden, activation= 'relu', input_dim=n_in))
model.add(Dense(n_hidden, activation= 'relu', input_dim=n_in))
model.add(Dense(n_hidden, activation= 'relu', input_dim=n_in))
model.add(Dense(units=n_out))
model.summary()
optimizer = Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
model.compile(loss='mean_squared_error', optimizer=optimizer)
# 学習オプション
history = model.fit(x_train, y_train, epochs=epochs, batch_size=batch_size, validation_data=(x_test, y_test))
# 構築したモデルで予測
test_predict = model.predict(x_test)
#精度評価指標
# MAE
test_MAE = mean_absolute_error(y_test, test_predict)
print('MAE:', test_MAE)
# MSE
test_MSE = mean_squared_error(y_test, test_predict)
print('MSE:', test_MSE)
# RMSE
test_RMSE = sqrt(mean_squared_error(y_test, test_predict))
print('RMSE:', test_RMSE)
# 決定係数
R2 = r2_score(y_test, test_predict)
print('R2:', R2)
# MAEに対するRMSEの比
print('RMSE/MAE:', test_RMSE / test_MAE)
# 損失関数
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = len(loss)
plt.plot(range(epochs), loss, marker='.', label='loss')
plt.plot(range(epochs), val_loss, marker='.', label='val_loss')
plt.legend(loc='best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
# Observed-Predicted Plot
plt.figure()
plt.scatter(y_test, test_predict, c='blue', alpha=0.8)
plt.ylim(plt.ylim())
plt.grid()
plt.xlabel('observed_data')
plt.ylabel('predicted_data')
plt.show()ちょい長めですが、順番に解説していきます。
ライブラリのインポート
# 使用するライブラリをインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import io
from google.colab import files
from sklearn.model_selection import train_test_split
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import Adam
from keras.callbacks import EarlyStopping, LearningRateScheduler
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from math import sqrt
from sklearn.metrics import r2_scoreまず、使用するライブラリをインポートしています。
あまり深く考える部分でもないので、適当にインポートしています。
データセットの読み込み
# Google Colaboratoryでファイルをアップロード
uploaded = files.upload()
# データフレームとして、変数dfに3列×10000行のデータを格納・確認
df = pd.read_csv(io.BytesIO(uploaded['data.csv']))
dfここでは、ローカルにあるcsvファイルをGoogle Colaboratoryにアップロードして、変数”df”にデータを格納しています。
ちなみに、ここの操作は以下の記事を参考にしました。

データの分割
# データの分割
(train, test) = train_test_split(df, test_size=0.2, shuffle=True)
# x_train, x_testではcsvファイルの1列目から2列目を,y_train, y_testでは3列目のデータを活用
x_train = train.iloc[:, [0, 1]]
y_train = train.iloc[:, [2]]
x_test = test.iloc[:, [0, 1]]
y_test = test.iloc[:, [2]]ここで、訓練データとテストデータに分けていきます。
上記のプログラムでは、訓練データ:テストデータ=8:2という形で分けていますが、「test_size=○○」の部分を変更すると比率は変わってきます。
また、1,2列目をインプットに、3列目をアウトプットとして、データを分割しています。
訓練データの正規化
# データの正規化
x_train = (x_train - x_train.min()) / (x_train.max() - x_train.min())
x_test = (x_test - x_test.min()) / (x_test.max() - x_test.min())データの正規化とは、データの最小値を0、最大値を1に変換する操作を指します。
訓練データを見ると、1列目の範囲は0〜10で、2列目の範囲は0〜1と、少し差があります。そのため、いい具合に調整するための操作です。
モデルの構築
# モデルの構築
# inputの数
n_in = 2
# ノードの数
n_hidden = 16
# outputの数
n_out = 1
# 学習回数
epochs = 50
batch_size = 64
model = Sequential()
model.add(Dense(n_hidden, activation= 'relu', input_dim=n_in))
model.add(Dense(n_hidden, activation= 'relu', input_dim=n_in))
model.add(Dense(n_hidden, activation= 'relu', input_dim=n_in))
model.add(Dense(units=n_out))
model.summary()
optimizer = Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
model.compile(loss='mean_squared_error', optimizer=optimizer)いよいよ、モデルの構築を行なっていきます。
上記のプログラムでは、中間層が3層で、各層のノード数は16としてニューラルネットワークを構築しています。
活性化関数はReLUを、最適化アルゴリズムはAdamを採用しています。
なお、ここの部分はKerasの公式が参考になります。
学習 → 予測
# 学習オプション
history = model.fit(x_train, y_train, epochs=epochs, batch_size=batch_size, validation_data=(x_test, y_test))上記コードを実行すると学習が始まります。
# 構築したモデルで予測
test_predict = model.predict(x_test)そして、構築したモデルから予測を行なっていきます。
精度評価指標
#精度評価指標
# MAE
test_MAE = mean_absolute_error(y_test, test_predict)
print('MAE:', test_MAE)
# MSE
test_MSE = mean_squared_error(y_test, test_predict)
print('MSE:', test_MSE)
# RMSE
test_RMSE = sqrt(mean_squared_error(y_test, test_predict))
print('RMSE:', test_RMSE)
# 決定係数
R2 = r2_score(y_test, test_predict)
print('R2:', R2)
# MAEに対するRMSEの比
print('RMSE/MAE:', test_RMSE / test_MAE)予測した値から、MAE、MSE、RMSE、決定係数を求めていきます。
ちなみに、実行した時は以下のようなデータが表示されます。
MAE: 0.02991514426947141 # 0に近いほど良い
MSE: 0.001563834395335399 # 0に近いほど良い
RMSE: 0.03954534606417548 # 0に近いほど良い
R2: 0.9988363429433301 # 1に近いほど良い
RMSE / MAE: 1.3219172773481072 # 1.253に近いほど良い詳細の数値は違うかもですが、おそらく似たような数値がでてくるはずです。
なお、この回帰分析の精度評価指標に関しては、以下の記事を参考にしました。
損失関数グラフの可視化
# 損失関数
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = len(loss)
plt.plot(range(epochs), loss, marker='.', label='loss')
plt.plot(range(epochs), val_loss, marker='.', label='val_loss')
plt.legend(loc='best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()上記コードを実行すると、損失関数のグラフをプロットすることができます。
なお、実際にプロットされたグラフは以下の通り。
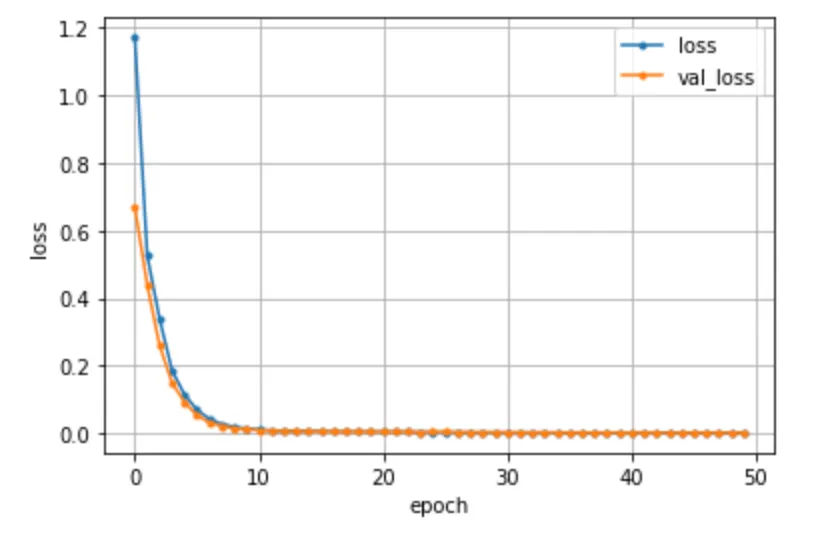
ここで、lossは訓練データに対する損失値を、val_lossはテストデータに対する損失値を示しています。
Observed-Predicted Plot
# Observed-Predicted Plot
plt.figure()
plt.scatter(y_test, test_predict, c='blue', alpha=0.8)
plt.ylim(plt.ylim())
plt.grid()
plt.xlabel('observed_data')
plt.ylabel('predicted_data')
plt.show()最後に、実データとの当てはまりの良さを調べるために、横軸に実測値を、縦軸に予測値をとったグラフをプロットします。
実際にプロットされたグラフは以下の通り。
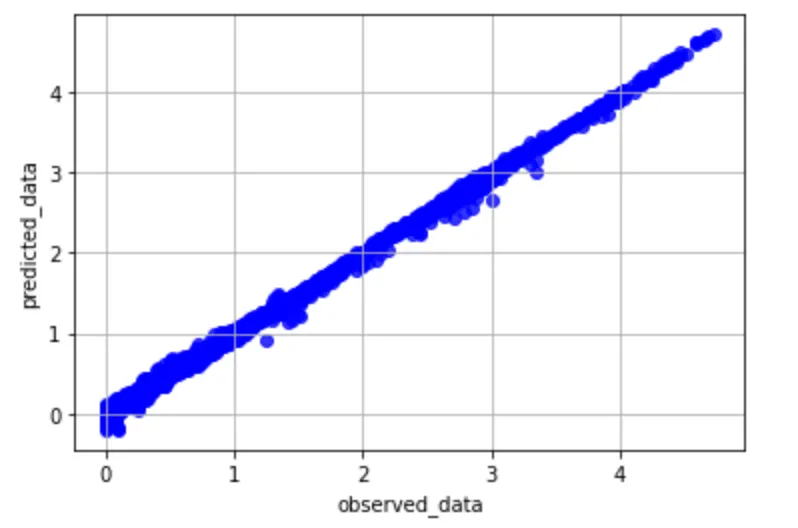
上記グラフのように、対角線上にプロットされていれば、良い予測が行えています。
以上、Kerasでニューラルネットワークを構築して、回帰分析を行うコードの解説でした。
Kerasで回帰ニューラルネットワークの実装まとめ

本記事では、Kerasの単純なSequentialモデルで、回帰分析を実行するニューラルネットワークの実装を解説しました。
本記事で紹介した参考記事もあわせつつ、興味ある方はぜひ実装してみてください。
また、今後ゆる〜いペースで機械学習に関する情報などを発信していくつもりなので、たまにみていただけると嬉しいです〜\(^o^)/